Regression standardization in Cox proportional hazards models

standardize_coxph performs regression standardization in Cox proportional hazards models at specified values of the exposure over the sample covariate distribution. Let $T$, $X$, and $Z$ be the survival outcome, the exposure, and a vector of covariates, respectively. standardize_coxph fits a Cox proportional hazards model and the Breslow estimator of the baseline hazard in order to estimate the standardized survival function $\theta(t,x)=E\{S(t|X=x,Z)\}$ when measure = "survival" or the standardized restricted mean survival up to time t $\theta(t, x) = E\{\int_0^t S(u|X = x, Z) du\}$ when measure = "rmean", where $t$ is a specific value of $T$, $x$ is a specific value of $X$, and the expectation is over the marginal distribution of $Z$.

Usage

standardize_coxph(
  formula,
  data,
  values,
  times,
  measure = c("survival", "rmean"),
  clusterid,
  ci_level = 0.95,
  ci_type = "plain",
  contrasts = NULL,
  family = "gaussian",
  reference = NULL,
  transforms = NULL
)

Arguments

formula: The formula which is used to fit the model for the outcome.
data: The data.
values: A named list or data.frame specifying the variables and values at which marginal means of the outcome will be estimated.
times: A vector containing the specific values of $T$ at which to estimate the standardized survival function.
measure: Either "survival" to estimate the survival function at times or "rmean" for the restricted mean survival up to the largest of times.
clusterid: An optional string containing the name of a cluster identification variable when data are clustered.
ci_level: Coverage probability of confidence intervals.
ci_type: A string, indicating the type of confidence intervals. Either "plain", which gives untransformed intervals, or "log", which gives log-transformed intervals.
contrasts: A vector of contrasts in the following format: If set to "difference" or "ratio", then $\psi(x)-\psi(x_0)$ or $\psi(x) / \psi(x_0)$ are constructed, where $x_0$ is a reference level specified by the reference argument. Has to be NULL if no references are specified.
family: The family argument which is used to fit the glm model for the outcome.
reference: A vector of reference levels in the following format: If contrasts is not NULL, the desired reference level(s). This must be a vector or list the same length as contrasts, and if not named, it is assumed that the order is as specified in contrasts.
transforms: A vector of transforms in the following format: If set to "log", "logit", or "odds", the standardized mean $\theta(x)$ is transformed into $\psi(x)=\log\{\theta(x)\}$, $\psi(x)=\log[\theta(x)/\{1-\theta(x)\}]$, or $\psi(x)=\theta(x)/\{1-\theta(x)\}$, respectively. If the vector is NULL, then $\psi(x)=\theta(x)$.

Value

An object of class std_surv. This is basically a list with components estimates and covariance estimates in res Results for transformations, contrasts, references are stored in res_contrasts. The output contains estimates for contrasts and confidence intervals for all combinations of transforms and reference levels. Obtain numeric results in a data frame with the tidy function.

Details

standardize_coxph fits the Cox proportional hazards model $$\lambda(t|X,Z)=\lambda_0(t)\exp\{h(X,Z;\beta)\}.$$ Breslow's estimator of the cumulative baseline hazard $\Lambda_0(t)=\int_0^t\lambda_0(u)du$ is used together with the partial likelihood estimate of $\beta$ to obtain estimates of the survival function $S(t|X=x,Z)$ if measure = "survival": $$\hat{S}(t|X=x,Z)=\exp[-\hat{\Lambda}_0(t)\exp\{h(X=x,Z;\hat{\beta})\}].$$ For each $t$ in the t argument and for each $x$ in the x argument, these estimates are averaged across all subjects (i.e. all observed values of $Z$) to produce estimates $$\hat{\theta}(t,x)=\sum_{i=1}^n \hat{S}(t|X=x,Z_i)/n,$$ where $Z_i$ is the value of $Z$ for subject $i$, $i=1,...,n$. The variance for $\hat{\theta}(t,x)$ is obtained by the sandwich formula.

If measure = "rmean", then $\Lambda_0(t)=\int_0^t\lambda_0(u)du$ is used together with the partial likelihood estimate of $\beta$ to obtain estimates of the restricted mean survival up to time t: $\int_0^t S(u|X=x,Z) du$ for each element of times. The estimation and inference is done using the method described in Chen and Tsiatis 2001. Currently, we can only estimate the difference in RMST for a single binary exposure. Two separate Cox models are fit for each level of the exposure, which is expected to be coded as 0/1.

Note

Standardized survival functions are sometimes referred to as (direct) adjusted survival functions in the literature.

standardize_coxph/standardize_parfrailty does not currently handle time-varying exposures or covariates.

standardize_coxph/standardize_parfrailty internally loops over all values in the t argument. Therefore, the function will usually be considerably faster if length(t) is small.

The variance calculation performed by standardize_coxph does not condition on the observed covariates $\bar{Z}=(Z_1,...,Z_n)$. To see how this matters, note that $$var\{\hat{\theta}(t,x)\}=E[var\{\hat{\theta}(t,x)|\bar{Z}\}]+var[E\{\hat{\theta}(t,x)|\bar{Z}\}].$$ The usual parameter $\beta$ in a Cox proportional hazards model does not depend on $\bar{Z}$. Thus, $E(\hat{\beta}|\bar{Z})$ is independent of $\bar{Z}$ as well (since $E(\hat{\beta}|\bar{Z})=\beta$), so that the term $var[E\{\hat{\beta}|\bar{Z}\}]$ in the corresponding variance decomposition for $var(\hat{\beta})$ becomes equal to 0. However, $\theta(t,x)$ depends on $\bar{Z}$ through the average over the sample distribution for $Z$, and thus the term $var[E\{\hat{\theta}(t,x)|\bar{Z}\}]$ is not 0, unless one conditions on $\bar{Z}$. The variance calculation by Gail and Byar (1986) ignores this term, and thus effectively conditions on $\bar{Z}$.

References

Chang I.M., Gelman G., Pagano M. (1982). Corrected group prognostic curves and summary statistics. Journal of Chronic Diseases 35, 669-674.

Gail M.H. and Byar D.P. (1986). Variance calculations for direct adjusted survival curves, with applications to testing for no treatment effect. Biometrical Journal 28(5), 587-599.

Makuch R.W. (1982). Adjusted survival curve estimation using covariates. Journal of Chronic Diseases 35, 437-443.

Sjölander A. (2016). Regression standardization with the R-package stdReg. European Journal of Epidemiology 31(6), 563-574.

Sjölander A. (2018). Estimation of causal effect measures with the R-package stdReg. European Journal of Epidemiology 33(9), 847-858.

Chen, P. Y., Tsiatis, A. A. (2001). Causal inference on the difference of the restricted mean lifetime between two groups. Biometrics, 57(4), 1030-1038.

Author

Arvid Sjölander, Adam Brand, Michael Sachs

Examples



require(survival)
set.seed(7)
n <- 300
Z <- rnorm(n)
Zbin <- rbinom(n, 1, .3)
X <- rnorm(n, mean = Z)
T <- rexp(n, rate = exp(X + Z + X * Z)) # survival time
C <- rexp(n, rate = exp(X + Z + X * Z)) # censoring time
fact <- factor(sample(letters[1:3], n, replace = TRUE))
U <- pmin(T, C) # time at risk
D <- as.numeric(T < C) # event indicator
dd <- data.frame(Z, Zbin, X, U, D, fact)
fit.std.surv <- standardize_coxph(
  formula = Surv(U, D) ~ X + Z + X * Z,
  data = dd,
  values = list(X = seq(-1, 1, 0.5)),
  times = 1:5
)
print(fit.std.surv)
#> 
#> Formula: Surv(U, D) ~ X + Z + X * Z
#> Exposure:  X 
#> Survival functions evaluated at t = 1 
#> 
#>        X Estimate Std.Error lower.0.95 upper 0.95
#> X   -1.0    0.750    0.0347      0.682      0.818
#> X.1 -0.5    0.589    0.0457      0.500      0.679
#> X.2  0.0    0.401    0.0387      0.325      0.477
#> X.3  0.5    0.295    0.0351      0.226      0.364
#> X.4  1.0    0.245    0.0343      0.178      0.312
#> 
#> 
#> Formula: Surv(U, D) ~ X + Z + X * Z
#> Exposure:  X 
#> Survival functions evaluated at t = 2 
#> 
#>        X Estimate Std.Error lower.0.95 upper 0.95
#> X   -1.0    0.529    0.0538     0.4238      0.635
#> X.1 -0.5    0.324    0.0498     0.2264      0.422
#> X.2  0.0    0.203    0.0349     0.1344      0.271
#> X.3  0.5    0.164    0.0320     0.1015      0.227
#> X.4  1.0    0.151    0.0311     0.0897      0.211
#> 
#> 
#> Formula: Surv(U, D) ~ X + Z + X * Z
#> Exposure:  X 
#> Survival functions evaluated at t = 3 
#> 
#>        X Estimate Std.Error lower.0.95 upper 0.95
#> X   -1.0    0.378    0.0631     0.2540      0.501
#> X.1 -0.5    0.188    0.0432     0.1029      0.272
#> X.2  0.0    0.123    0.0307     0.0626      0.183
#> X.3  0.5    0.111    0.0287     0.0549      0.167
#> X.4  1.0    0.110    0.0282     0.0552      0.166
#> 
#> 
#> Formula: Surv(U, D) ~ X + Z + X * Z
#> Exposure:  X 
#> Survival functions evaluated at t = 4 
#> 
#>        X Estimate Std.Error lower.0.95 upper 0.95
#> X   -1.0   0.2959    0.0662     0.1661      0.426
#> X.1 -0.5   0.1287    0.0392     0.0519      0.205
#> X.2  0.0   0.0902    0.0288     0.0337      0.147
#> X.3  0.5   0.0884    0.0273     0.0348      0.142
#> X.4  1.0   0.0925    0.0272     0.0393      0.146
#> 
#> 
#> Formula: Surv(U, D) ~ X + Z + X * Z
#> Exposure:  X 
#> Survival functions evaluated at t = 5 
#> 
#>        X Estimate Std.Error lower.0.95 upper 0.95
#> X   -1.0   0.2255    0.0657     0.0967      0.354
#> X.1 -0.5   0.0857    0.0328     0.0214      0.150
#> X.2  0.0   0.0663    0.0251     0.0170      0.116
#> X.3  0.5   0.0707    0.0247     0.0223      0.119
#> X.4  1.0   0.0781    0.0251     0.0288      0.127
#> 
plot(fit.std.surv)

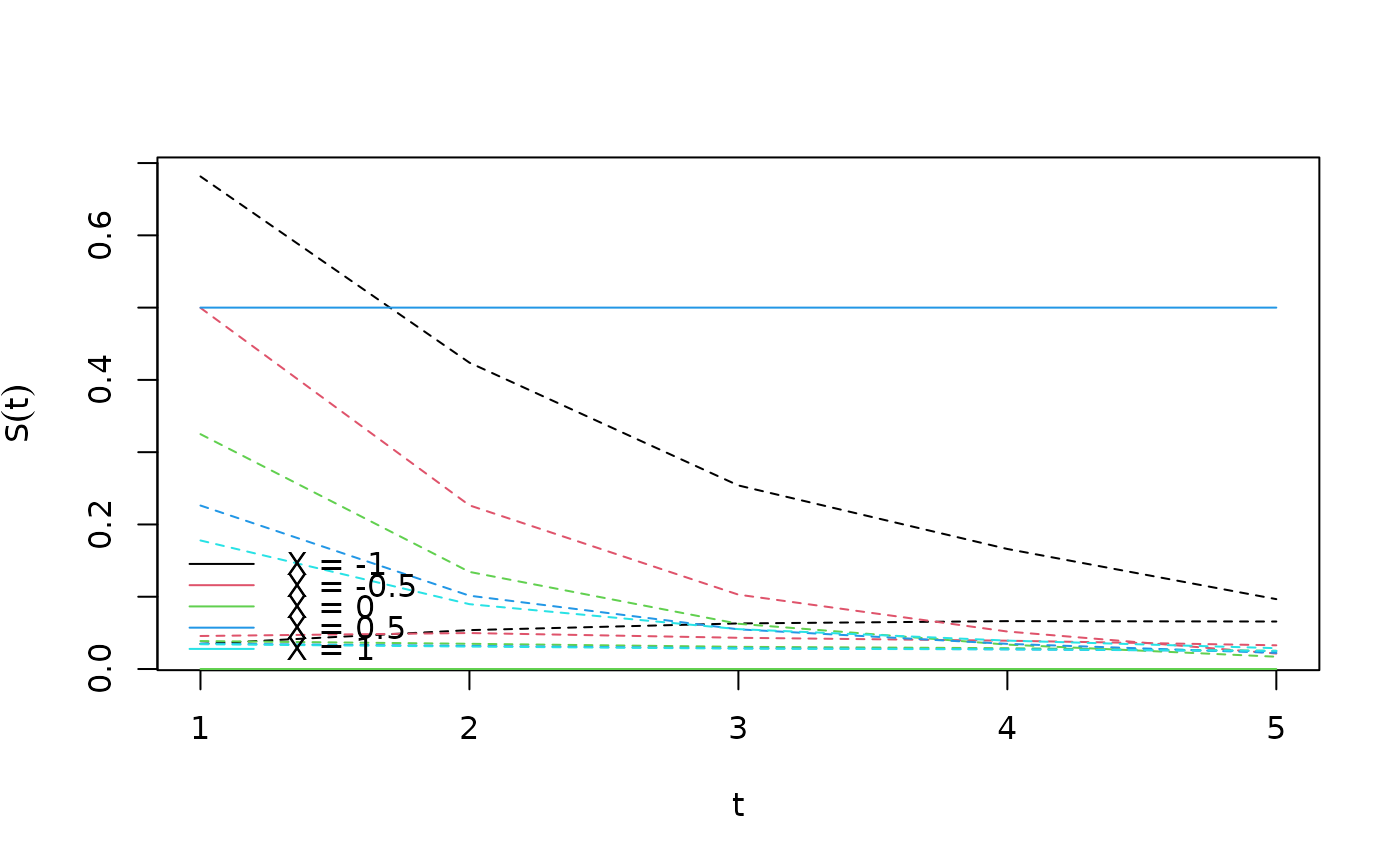tidy(fit.std.surv)
#>         X   Estimate  Std.Error lower.0.95 upper.0.95 time contrast transform
#> X    -1.0 0.74957538 0.03473035 0.68150514  0.8176456    1     none  identity
#> X.1  -0.5 0.58923837 0.04569250 0.49968272  0.6787940    1     none  identity
#> X.2   0.0 0.40080421 0.03870365 0.32494645  0.4766620    1     none  identity
#> X.3   0.5 0.29503631 0.03511907 0.22620419  0.3638684    1     none  identity
#> X.4   1.0 0.24509832 0.03430180 0.17786802  0.3123286    1     none  identity
#> X1   -1.0 0.52930785 0.05380874 0.42384466  0.6347710    2     none  identity
#> X.11 -0.5 0.32403918 0.04979327 0.22644617  0.4216322    2     none  identity
#> X.21  0.0 0.20279513 0.03490407 0.13438441  0.2712058    2     none  identity
#> X.31  0.5 0.16421470 0.03202055 0.10145557  0.2269738    2     none  identity
#> X.41  1.0 0.15059296 0.03105317 0.08972986  0.2114561    2     none  identity
#> X2   -1.0 0.37756823 0.06305952 0.25397385  0.5011626    3     none  identity
#> X.12 -0.5 0.18758405 0.04321095 0.10289215  0.2722760    3     none  identity
#> X.22  0.0 0.12278095 0.03071049 0.06258949  0.1829724    3     none  identity
#> X.32  0.5 0.11114345 0.02869313 0.05490595  0.1673810    3     none  identity
#> X.42  1.0 0.11048888 0.02821866 0.05518133  0.1657964    3     none  identity
#> X3   -1.0 0.29592579 0.06624722 0.16608364  0.4257679    4     none  identity
#> X.13 -0.5 0.12866612 0.03918314 0.05186858  0.2054637    4     none  identity
#> X.23  0.0 0.09021194 0.02881483 0.03373592  0.1466880    4     none  identity
#> X.33  0.5 0.08837564 0.02733102 0.03480782  0.1419435    4     none  identity
#> X.43  1.0 0.09253934 0.02716367 0.03929953  0.1457792    4     none  identity
#> X4   -1.0 0.22546407 0.06571110 0.09667268  0.3542555    5     none  identity
#> X.14 -0.5 0.08572099 0.03280939 0.02141577  0.1500262    5     none  identity
#> X.24  0.0 0.06626788 0.02513536 0.01700349  0.1155323    5     none  identity
#> X.34  0.5 0.07069841 0.02469322 0.02230060  0.1190962    5     none  identity
#> X.44  1.0 0.07810587 0.02513514 0.02884189  0.1273698    5     none  identity
#>       measure
#> X    survival
#> X.1  survival
#> X.2  survival
#> X.3  survival
#> X.4  survival
#> X1   survival
#> X.11 survival
#> X.21 survival
#> X.31 survival
#> X.41 survival
#> X2   survival
#> X.12 survival
#> X.22 survival
#> X.32 survival
#> X.42 survival
#> X3   survival
#> X.13 survival
#> X.23 survival
#> X.33 survival
#> X.43 survival
#> X4   survival
#> X.14 survival
#> X.24 survival
#> X.34 survival
#> X.44 survival

fit.std <- standardize_coxph(
  formula = Surv(U, D) ~ X + Zbin + X * Zbin + fact,
  data = dd,
  values = list(Zbin = 0:1),
  times = 1.5,
  measure = "rmean",
  contrast = "difference",
  reference = 0
)
print(fit.std)
#> 
#> Formula: Surv(U, D) ~ X + fact
#>  Fit separately by exposure 
#> Exposure:  Zbin 
#> Restricted mean survival evaluated at t = 1.5 
#> 
#>   Zbin Estimate Std.Error lower.0.95 upper 0.95
#> 1    0    0.716    0.0447      0.628      0.804
#> 2    1    0.667    0.0542      0.561      0.773
#> 
#> 
#> Formula: Surv(U, D) ~ X + fact
#>  Fit separately by exposure 
#> Exposure:  Zbin 
#> Reference level:  = 0 
#> Contrast:  difference 
#> Restricted mean survival evaluated at t = 1.5 
#> 
#>   Zbin Estimate Std.Error lower.0.95 upper 0.95
#> 1    0   0.0000    0.0000      0.000     0.0000
#> 2    1  -0.0489    0.0608     -0.168     0.0703
#> 
tidy(fit.std)
#>   Zbin    Estimate  Std.Error lower.0.95 upper.0.95 time   contrast transform
#> 1    0  0.71593627 0.04471627  0.6282940 0.80357854  1.5       none  identity
#> 2    1  0.66701532 0.05419799  0.5607892 0.77324143  1.5       none  identity
#> 3    0  0.00000000 0.00000000  0.0000000 0.00000000  1.5 difference  identity
#> 4    1 -0.04892094 0.06084537 -0.1681757 0.07033379  1.5 difference  identity
#>   measure
#> 1   rmean
#> 2   rmean
#> 3   rmean
#> 4   rmean