Regression standardization in conditional generalized estimating equations

standardize_gee performs regression standardization in linear and log-linear fixed effects models, at specified values of the exposure, over the sample covariate distribution. Let $Y$, $X$, and $Z$ be the outcome, the exposure, and a vector of covariates, respectively. It is assumed that data are clustered with a cluster indicator $i$. standardize_gee uses fitted fixed effects model, with cluster-specific intercept $a_i$ (see details), to estimate the standardized mean $\theta(x)=E\{E(Y|i,X=x,Z)\}$, where $x$ is a specific value of $X$, and the outer expectation is over the marginal distribution of $(a_i,Z)$.

Usage

standardize_gee(
  formula,
  link = "identity",
  data,
  values,
  clusterid,
  case_control = FALSE,
  ci_level = 0.95,
  ci_type = "plain",
  contrasts = NULL,
  family = "gaussian",
  reference = NULL,
  transforms = NULL
)

Arguments

formula: A formula to be used with "gee" in the drgee package.
link: The link function to be used with "gee".
data: The data.
values: A named list or data.frame specifying the variables and values at which marginal means of the outcome will be estimated.
clusterid: An optional string containing the name of a cluster identification variable when data are clustered.
case_control: Whether the data comes from a case-control study.
ci_level: Coverage probability of confidence intervals.
ci_type: A string, indicating the type of confidence intervals. Either "plain", which gives untransformed intervals, or "log", which gives log-transformed intervals.
contrasts: A vector of contrasts in the following format: If set to "difference" or "ratio", then $\psi(x)-\psi(x_0)$ or $\psi(x) / \psi(x_0)$ are constructed, where $x_0$ is a reference level specified by the reference argument. Has to be NULL if no references are specified.
family: The family argument which is used to fit the glm model for the outcome.
reference: A vector of reference levels in the following format: If contrasts is not NULL, the desired reference level(s). This must be a vector or list the same length as contrasts, and if not named, it is assumed that the order is as specified in contrasts.
transforms: A vector of transforms in the following format: If set to "log", "logit", or "odds", the standardized mean $\theta(x)$ is transformed into $\psi(x)=\log\{\theta(x)\}$, $\psi(x)=\log[\theta(x)/\{1-\theta(x)\}]$, or $\psi(x)=\theta(x)/\{1-\theta(x)\}$, respectively. If the vector is NULL, then $\psi(x)=\theta(x)$.

Value

An object of class std_glm. This is basically a list with components estimates and covariance estimates in res. Results for transformations, contrasts, references are stored in res_contrasts. Obtain numeric results in a data frame with the tidy function.

Details

standardize_gee assumes that a fixed effects model $$\eta\{E(Y|i,X,Z)\}=a_i+h(X,Z;\beta)$$ has been fitted. The link function $\eta$ is assumed to be the identity link or the log link. The conditional generalized estimating equation (CGEE) estimate of $\beta$ is used to obtain estimates of the cluster-specific means: $$\hat{a}_i=\sum_{j=1}^{n_i}r_{ij}/n_i,$$ where $$r_{ij}=Y_{ij}-h(X_{ij},Z_{ij};\hat{\beta})$$ if $\eta$ is the identity link, and $$r_{ij}=Y_{ij}\exp\{-h(X_{ij},Z_{ij};\hat{\beta})\}$$ if $\eta$ is the log link, and $(X_{ij},Z_{ij})$ is the value of $(X,Z)$ for subject $j$ in cluster $i$, $j=1,...,n_i$, $i=1,...,n$. The CGEE estimate of $\beta$ and the estimate of $a_i$ are used to estimate the mean $E(Y|i,X=x,Z)$: $$\hat{E}(Y|i,X=x,Z)=\eta^{-1}\{\hat{a}_i+h(X=x,Z;\hat{\beta})\}.$$ For each $x$ in the x argument, these estimates are averaged across all subjects (i.e. all observed values of $Z$ and all estimated values of $a_i$) to produce estimates $$\hat{\theta}(x)=\sum_{i=1}^n \sum_{j=1}^{n_i} \hat{E}(Y|i,X=x,Z_i)/N,$$ where $N=\sum_{i=1}^n n_i$. The variance for $\hat{\theta}(x)$ is obtained by the sandwich formula.

Note

The variance calculation performed by standardize_gee does not condition on the observed covariates $\bar{Z}=(Z_{11},...,Z_{nn_i})$. To see how this matters, note that $$var\{\hat{\theta}(x)\}=E[var\{\hat{\theta}(x)|\bar{Z}\}]+var[E\{\hat{\theta}(x)|\bar{Z}\}].$$ The usual parameter $\beta$ in a generalized linear model does not depend on $\bar{Z}$. Thus, $E(\hat{\beta}|\bar{Z})$ is independent of $\bar{Z}$ as well (since $E(\hat{\beta}|\bar{Z})=\beta$), so that the term $var[E\{\hat{\beta}|\bar{Z}\}]$ in the corresponding variance decomposition for $var(\hat{\beta})$ becomes equal to 0. However, $\theta(x)$ depends on $\bar{Z}$ through the average over the sample distribution for $Z$, and thus the term $var[E\{\hat{\theta}(x)|\bar{Z}\}]$ is not 0, unless one conditions on $\bar{Z}$.

References

Goetgeluk S. and Vansteelandt S. (2008). Conditional generalized estimating equations for the analysis of clustered and longitudinal data. Biometrics 64(3), 772-780.

Martin R.S. (2017). Estimation of average marginal effects in multiplicative unobserved effects panel models. Economics Letters 160, 16-19.

Sjölander A. (2019). Estimation of marginal causal effects in the presence of confounding by cluster. Biostatistics doi: 10.1093/biostatistics/kxz054

Author

Arvid Sjölander.

Examples


require(drgee)
#> Loading required package: drgee

set.seed(4)
n <- 300
ni <- 2
id <- rep(1:n, each = ni)
ai <- rep(rnorm(n), each = ni)
Z <- rnorm(n * ni)
X <- rnorm(n * ni, mean = ai + Z)
Y <- rnorm(n * ni, mean = ai + X + Z + 0.1 * X^2)
dd <- data.frame(id, Z, X, Y)
fit.std <- standardize_gee(
  formula = Y ~ X + Z + I(X^2),
  link = "identity",
  data = dd,
  values = list(X = seq(-3, 3, 0.5)),
  clusterid = "id"
)
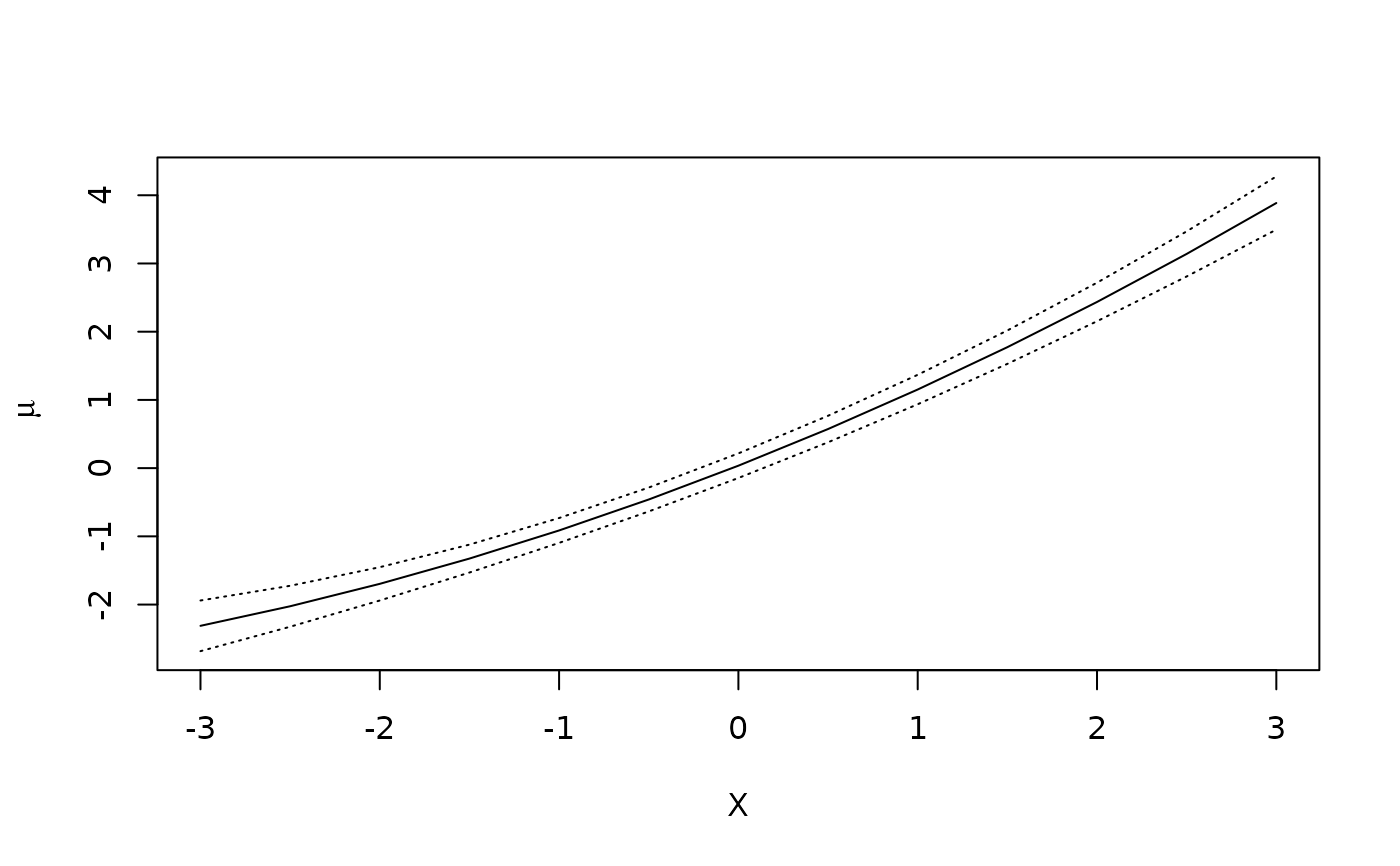
print(fit.std)
#> Outcome formula: Y ~ X + Z + I(X^2)
#> <environment: 0x63e94b15ac28>
#> Outcome family: 
#> Outcome link function: 
#> Exposure:  X 
#> 
#> Tables: 
#>       X Estimate Std.Error lower.0.95 upper.0.95
#> 1  -3.0  -2.3117    0.1895     -2.683     -1.940
#> 2  -2.5  -2.0248    0.1531     -2.325     -1.725
#> 3  -2.0  -1.6962    0.1246     -1.940     -1.452
#> 4  -1.5  -1.3258    0.1045     -1.531     -1.121
#> 5  -1.0  -0.9137    0.0930     -1.096     -0.731
#> 6  -0.5  -0.4598    0.0894     -0.635     -0.285
#> 7   0.0   0.0358    0.0920     -0.144      0.216
#> 8   0.5   0.5732    0.0991      0.379      0.767
#> 9   1.0   1.1523    0.1101      0.936      1.368
#> 10  1.5   1.7731    0.1249      1.528      2.018
#> 11  2.0   2.4357    0.1442      2.153      2.718
#> 12  2.5   3.1401    0.1686      2.810      3.471
#> 13  3.0   3.8862    0.1989      3.496      4.276
#> 
plot(fit.std)