Get regression standardized estimates from a glm

Usage

standardize_glm(
  formula,
  data,
  values,
  clusterid,
  matched_density_cases,
  matched_density_controls,
  matching_variable,
  p_population,
  case_control = FALSE,
  ci_level = 0.95,
  ci_type = "plain",
  contrasts = NULL,
  family = "gaussian",
  reference = NULL,
  transforms = NULL
)

Arguments

formula: The formula which is used to fit the model for the outcome.
data: The data.
values: A named list or data.frame specifying the variables and values at which marginal means of the outcome will be estimated.
clusterid: An optional string containing the name of a cluster identification variable when data are clustered.
matched_density_cases: A function of the matching variable. The probability (or density) of the matched variable among the cases.
matched_density_controls: A function of the matching variable. The probability (or density) of the matched variable among the controls.
matching_variable: The matching variable extracted from the data set.
p_population: Specifies the incidence in the population when case_control=TRUE.
case_control: Whether the data comes from a case-control study.
ci_level: Coverage probability of confidence intervals.
ci_type: A string, indicating the type of confidence intervals. Either "plain", which gives untransformed intervals, or "log", which gives log-transformed intervals.
contrasts: A vector of contrasts in the following format: If set to "difference" or "ratio", then \(\psi(x)-\psi(x_0)\) or \(\psi(x) / \psi(x_0)\) are constructed, where \(x_0\) is a reference level specified by the reference argument. Has to be NULL if no references are specified.
family: The family argument which is used to fit the glm model for the outcome.
reference: A vector of reference levels in the following format: If contrasts is not NULL, the desired reference level(s). This must be a vector or list the same length as contrasts, and if not named, it is assumed that the order is as specified in contrasts.
transforms: A vector of transforms in the following format: If set to "log", "logit", or "odds", the standardized mean \(\theta(x)\) is transformed into \(\psi(x)=\log\{\theta(x)\}\), \(\psi(x)=\log[\theta(x)/\{1-\theta(x)\}]\), or \(\psi(x)=\theta(x)/\{1-\theta(x)\}\), respectively. If the vector is NULL, then \(\psi(x)=\theta(x)\).

Value

An object of class std_glm. Obtain numeric results in a data frame with the tidy.std_glm function. This is a list with the following components:

res_contrast

An unnamed list with one element for each of the requested contrasts. Each element is itself a list with the elements:

estimates: Estimated counterfactual means and standard errors for each exposure level
covariance: Estimated covariance matrix of counterfactual means
fit_outcome: The estimated regression model for the outcome
fit_exposure: The estimated exposure model
exposure_names: A character vector of the exposure variable names
est_table: Data.frame of the estimates of the contrast with inference
transform: The transform argument used for this contrast
contrast: The requested contrast type
reference: The reference level of the exposure
ci_type: Confidence interval type
ci_level: Confidence interval level

res

A named list with the elements:

estimates: Estimated counterfactual means and standard errors for each exposure level
covariance: Estimated covariance matrix of counterfactual means
fit_outcome: The estimated regression model for the outcome
fit_exposure: The estimated exposure model
exposure_names: A character vector of the exposure variable names

Details

standardize_glm performs regression standardization in generalized linear models, at specified values of the exposure, over the sample covariate distribution. Let \(Y\), \(X\), and \(Z\) be the outcome, the exposure, and a vector of covariates, respectively. standardize_glm uses a fitted generalized linear model to estimate the standardized mean \(\theta(x)=E\{E(Y|X=x,Z)\}\), where \(x\) is a specific value of \(X\), and the outer expectation is over the marginal distribution of \(Z\).

References

Rothman K.J., Greenland S., Lash T.L. (2008). Modern Epidemiology, 3rd edition. Lippincott, Williams & Wilkins.

Sjölander A. (2016). Regression standardization with the R-package stdReg. European Journal of Epidemiology 31(6), 563-574.

Sjölander A. (2016). Estimation of causal effect measures with the R-package stdReg. European Journal of Epidemiology 33(9), 847-858.

Examples


# basic example
# needs to correctly specify the outcome model and no unmeasered confounders
# (+ standard causal assunmptions)
set.seed(6)
n <- 100
Z <- rnorm(n)
X <- cut(rnorm(n, mean = Z), breaks = c(-Inf, 0, Inf), labels = c("low", "high"))
Y <- rbinom(n, 1, prob = (1 + exp(as.numeric(X) + Z))^(-1))
dd <- data.frame(Z, X, Y)
x <- standardize_glm(
  formula = Y ~ X * Z,
  family = "binomial",
  data = dd,
  values = list(X = c("low", "high")),
  contrasts = c("difference", "ratio"),
  reference = "low"
)
x
#> Outcome formula: Y ~ X * Z
#> <environment: 0x58fe73017f40>
#> Outcome family: quasibinomial 
#> Outcome link function: logit 
#> Exposure:  X 
#> 
#> Tables: 
#>      X Estimate Std.Error lower.0.95 upper.0.95
#> 1  low    0.286    0.0514     0.1850      0.386
#> 2 high    0.198    0.1128    -0.0234      0.419
#> 
#> Reference level:  X = low 
#> Contrast:  difference 
#>      X Estimate Std.Error lower.0.95 upper.0.95
#> 1  low    0.000      0.00      0.000      0.000
#> 2 high   -0.088      0.12     -0.324      0.148
#> 
#> Reference level:  X = low 
#> Contrast:  ratio 
#>      X Estimate Std.Error lower.0.95 upper.0.95
#> 1  low    1.000     0.000      1.000       1.00
#> 2 high    0.692     0.404     -0.101       1.48
#> 
# different transformations of causal effects

# example from Sjölander (2016) with case-control data
# here the matching variable needs to be passed as an argument
singapore <- AF::singapore
#> Registered S3 methods overwritten by 'stdReg':
#>   method                   from   
#>   summary.parfrailty       stdReg2
#>   print.summary.parfrailty stdReg2
Mi <- singapore$Age
m <- mean(Mi)
s <- sd(Mi)
d <- 5
standardize_glm(
  formula = Oesophagealcancer ~ (Everhotbev + Age + Dial + Samsu + Cigs)^2,
  family = binomial, data = singapore,
  values = list(Everhotbev = 0:1), clusterid = "Set",
  case_control = TRUE,
  matched_density_cases = function(x) dnorm(x, m, s),
  matched_density_controls = function(x) dnorm(x, m - d, s),
  matching_variable = Mi,
  p_population = 19.3 / 100000
)
#> Warning: case_control = TRUE may not give reasonable results for the variance with clustering
#> Outcome formula: Oesophagealcancer ~ (Everhotbev + Age + Dial + Samsu + Cigs)^2
#> <environment: 0x58fe73017f40>
#> Outcome family: quasibinomial 
#> Outcome link function: logit 
#> Exposure:  Everhotbev 
#> 
#> Tables: 
#>   Everhotbev Estimate Std.Error lower.0.95 upper.0.95
#> 1          0 0.000128  2.27e-05   8.33e-05   0.000172
#> 2          1 0.000570  2.26e-04   1.27e-04   0.001014
#> 

# multiple exposures
set.seed(7)
n <- 100
Z <- rnorm(n)
X1 <- rnorm(n, mean = Z)
X2 <- rnorm(n)
Y <- rbinom(n, 1, prob = (1 + exp(X1 + X2 + Z))^(-1))
dd <- data.frame(Z, X1, X2, Y)
x <- standardize_glm(
  formula = Y ~ X1 + X2 + Z,
  family = "binomial",
  data = dd, values = list(X1 = 0:1, X2 = 0:1),
  contrasts = c("difference", "ratio"),
  reference = c(X1 = 0, X2 = 0)
)
x
#> Outcome formula: Y ~ X1 + X2 + Z
#> <environment: 0x58fe73017f40>
#> Outcome family: quasibinomial 
#> Outcome link function: logit 
#> Exposure:  X1, X2 
#> 
#> Tables: 
#>   X1 X2 Estimate Std.Error lower.0.95 upper.0.95
#> 1  0  0    0.419    0.0599    0.30143      0.536
#> 2  1  0    0.252    0.0745    0.10637      0.398
#> 3  0  1    0.273    0.0734    0.12947      0.417
#> 4  1  1    0.146    0.0719    0.00477      0.287
#> 
#> Reference level:  X1 = 0; X2 = 0 
#> Contrast:  difference 
#>   X1 X2 Estimate Std.Error lower.0.95 upper.0.95
#> 1  0  0    0.000    0.0000      0.000     0.0000
#> 2  1  0   -0.166    0.0704     -0.304    -0.0284
#> 3  0  1   -0.145    0.0501     -0.244    -0.0473
#> 4  1  1   -0.273    0.0745     -0.419    -0.1271
#> 
#> Reference level:  X1 = 0; X2 = 0 
#> Contrast:  ratio 
#>   X1 X2 Estimate Std.Error lower.0.95 upper.0.95
#> 1  0  0    1.000     0.000     1.0000      1.000
#> 2  1  0    0.603     0.157     0.2946      0.911
#> 3  0  1    0.653     0.124     0.4098      0.896
#> 4  1  1    0.348     0.160     0.0344      0.661
#> 
tidy(x)
#>    X1 X2   Estimate  Std.Error   lower.0.95  upper.0.95   contrast transform
#> 1   0  0  0.4187976 0.05988132  0.301432401  0.53616285       none  identity
#> 2   1  0  0.2523918 0.07450114  0.106372210  0.39841133       none  identity
#> 3   0  1  0.2733894 0.07342930  0.129470661  0.41730822       none  identity
#> 4   1  1  0.1456809 0.07189265  0.004773882  0.28658788       none  identity
#> 5   0  0  0.0000000 0.00000000  0.000000000  0.00000000 difference  identity
#> 6   1  0 -0.1664059 0.07039483 -0.304377189 -0.02843452 difference  identity
#> 7   0  1 -0.1454082 0.05007717 -0.243557635 -0.04725874 difference  identity
#> 8   1  1 -0.2731167 0.07448750 -0.419109552 -0.12712394 difference  identity
#> 9   0  0  1.0000000 0.00000000  1.000000000  1.00000000      ratio  identity
#> 10  1  0  0.6026581 0.15718090  0.294589170  0.91072698      ratio  identity
#> 11  0  1  0.6527961 0.12398991  0.409780305  0.89581181      ratio  identity
#> 12  1  1  0.3478551 0.15995045  0.034357954  0.66135220      ratio  identity

# continuous exposure
set.seed(2)
n <- 100
Z <- rnorm(n)
X <- rnorm(n, mean = Z)
Y <- rnorm(n, mean = X + Z + 0.1 * X^2)
dd <- data.frame(Z, X, Y)
x <- standardize_glm(
  formula = Y ~ X * Z,
  family = "gaussian",
  data = dd,
  values = list(X = seq(-1, 1, 0.1))
)

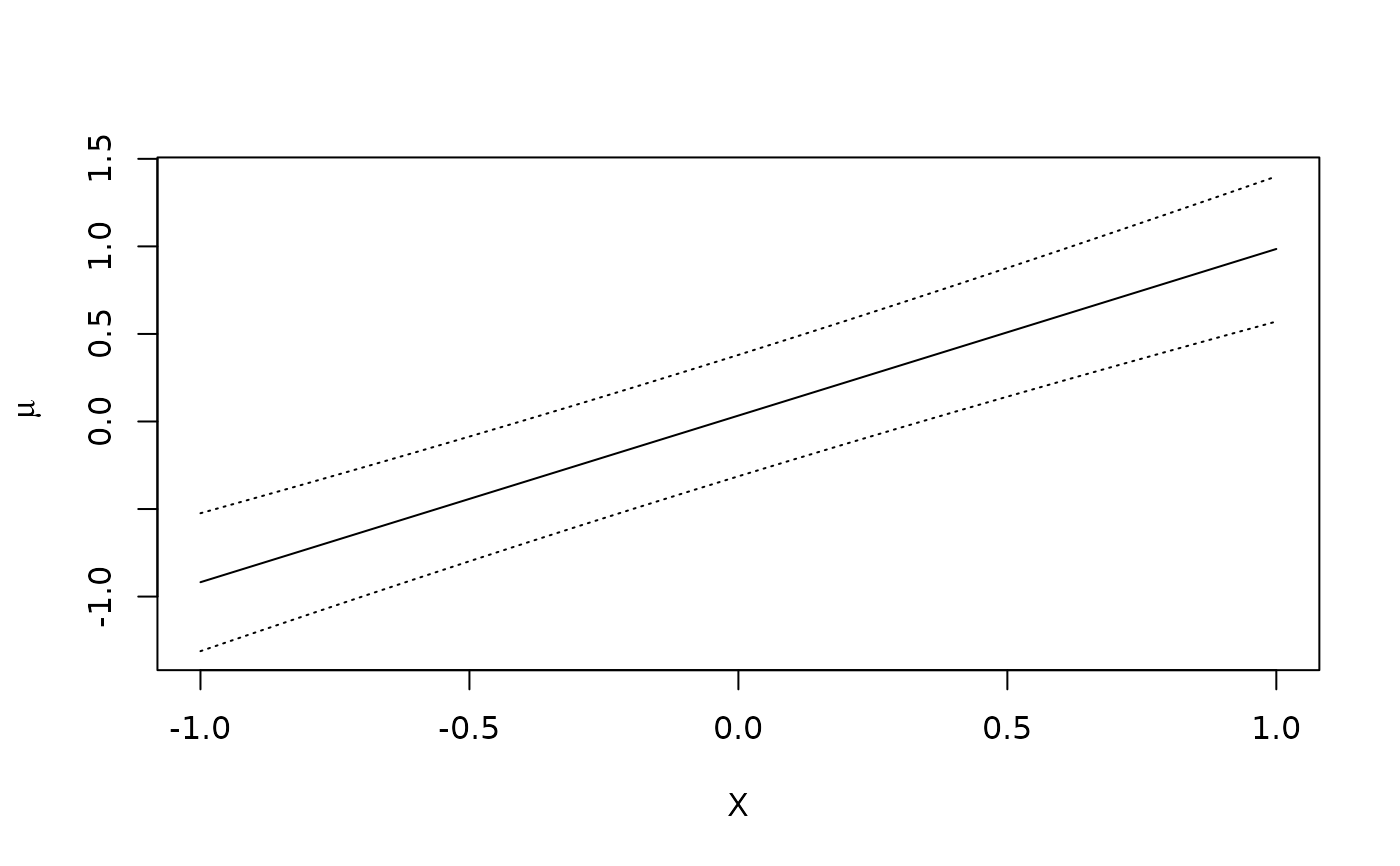
# plot standardized mean as a function of x
plot(x)

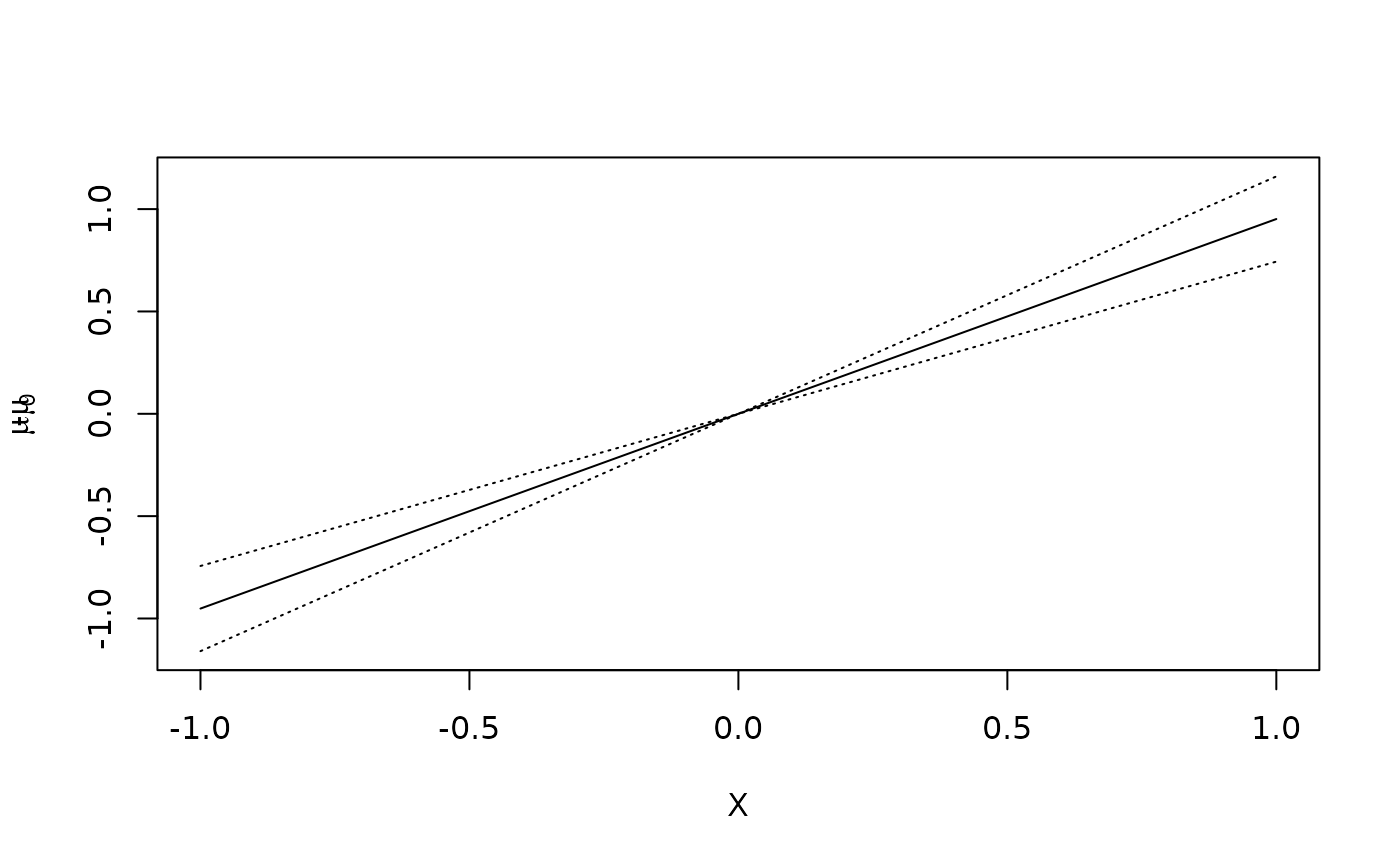
# plot standardized mean - standardized mean at x = 0 as a function of x
plot(x, contrast = "difference", reference = 0)