Joint modelling multiple endpoints

Learning objectives

In this lesson you will

1. Write a function to perform simultaneous inference for covariate effects on multiple outcomes in the competing risks setting.

Setup

Library the survival package and then the eventglm package, and then the geepack package.

library(survival)
library(eventglm)
library(geepack)

Joint models

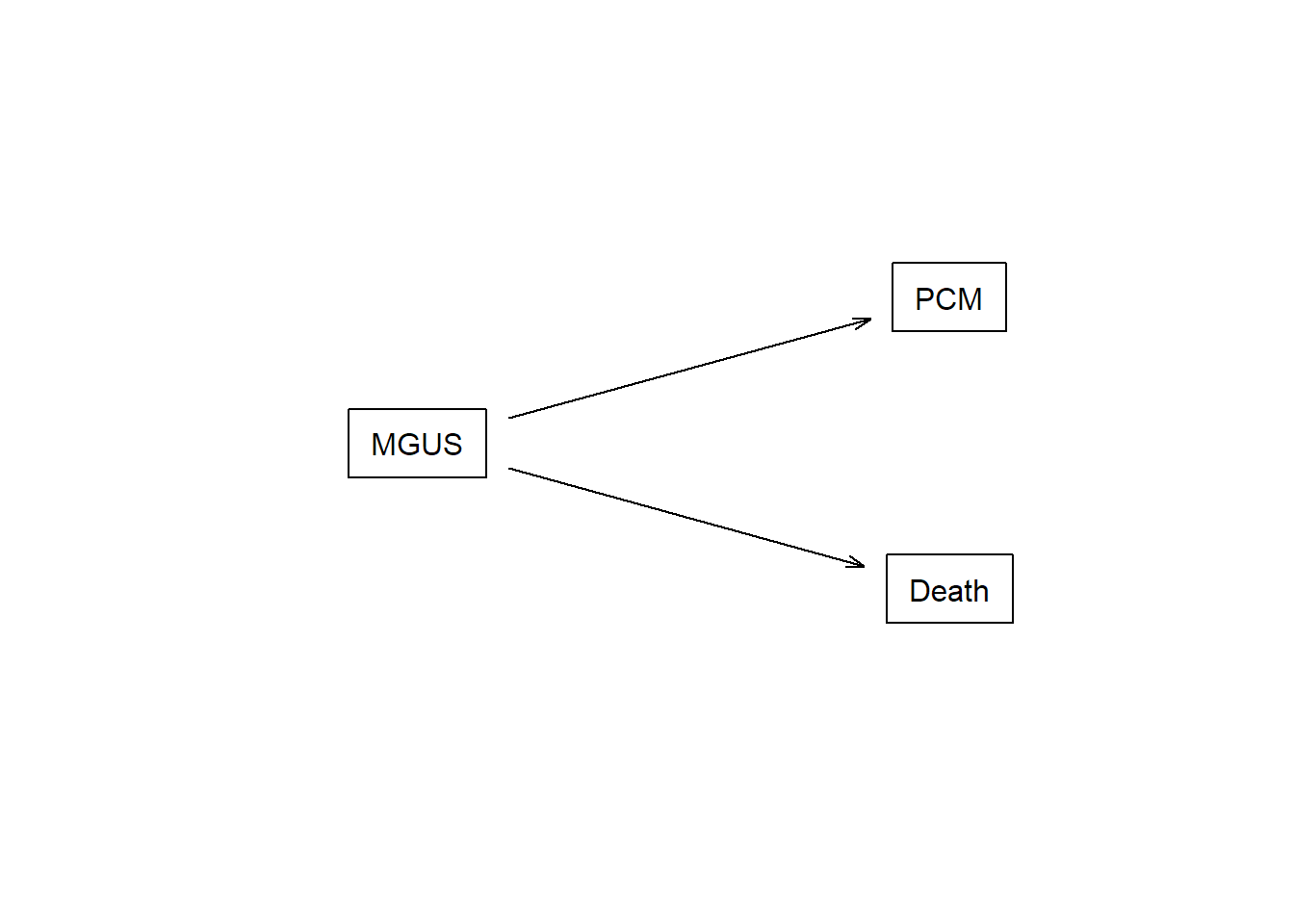
Consider again the mgus2 dataset. This is a competing risks setting, with the two possible causes of failure: death and pcm.

crfit <- survfit(Surv(etime, event) ~ sex, eventglm::mgus2)
summary(crfit, times = 120)

## Call: survfit(formula = Surv(etime, event) ~ sex, data = eventglm::mgus2)
## 
##                 sex=F 
##     time   n.risk  n.event  P((s0))   P(pcm) P(death) 
## 120.0000 214.0000 331.0000   0.4456   0.0739   0.4805 
## 
##                 sex=M 
##     time   n.risk  n.event  P((s0))   P(pcm) P(death) 
## 120.0000 210.0000 450.0000   0.3695   0.0553   0.5752

print(crfit, rmean = 120)

## Call: survfit(formula = Surv(etime, event) ~ sex, data = eventglm::mgus2)
## 
##                n nevent    rmean*
## sex=F, (s0)  631      0 82.983485
## sex=M, (s0)  753      0 74.808346
## sex=F, pcm   631     59  4.794595
## sex=M, pcm   753     56  3.501305
## sex=F, death 631    370 32.221921
## sex=M, death 753    490 41.690349
##    *mean time in state, restricted (max time = 120 )

plot(crfit, col=1:2,  noplot="",
     lty=c(3,3,2,2,1,1), lwd=2, xscale=12,
     xlab="Years post diagnosis", ylab="P(state)")
legend(240, .65, c("Female, death", "Male, death", "malignancy", "(s0)"),
       lty=c(1,1,2,3), col=c(1,2,1,1), bty='n', lwd=2)
abline(v = 120, lty = 2)

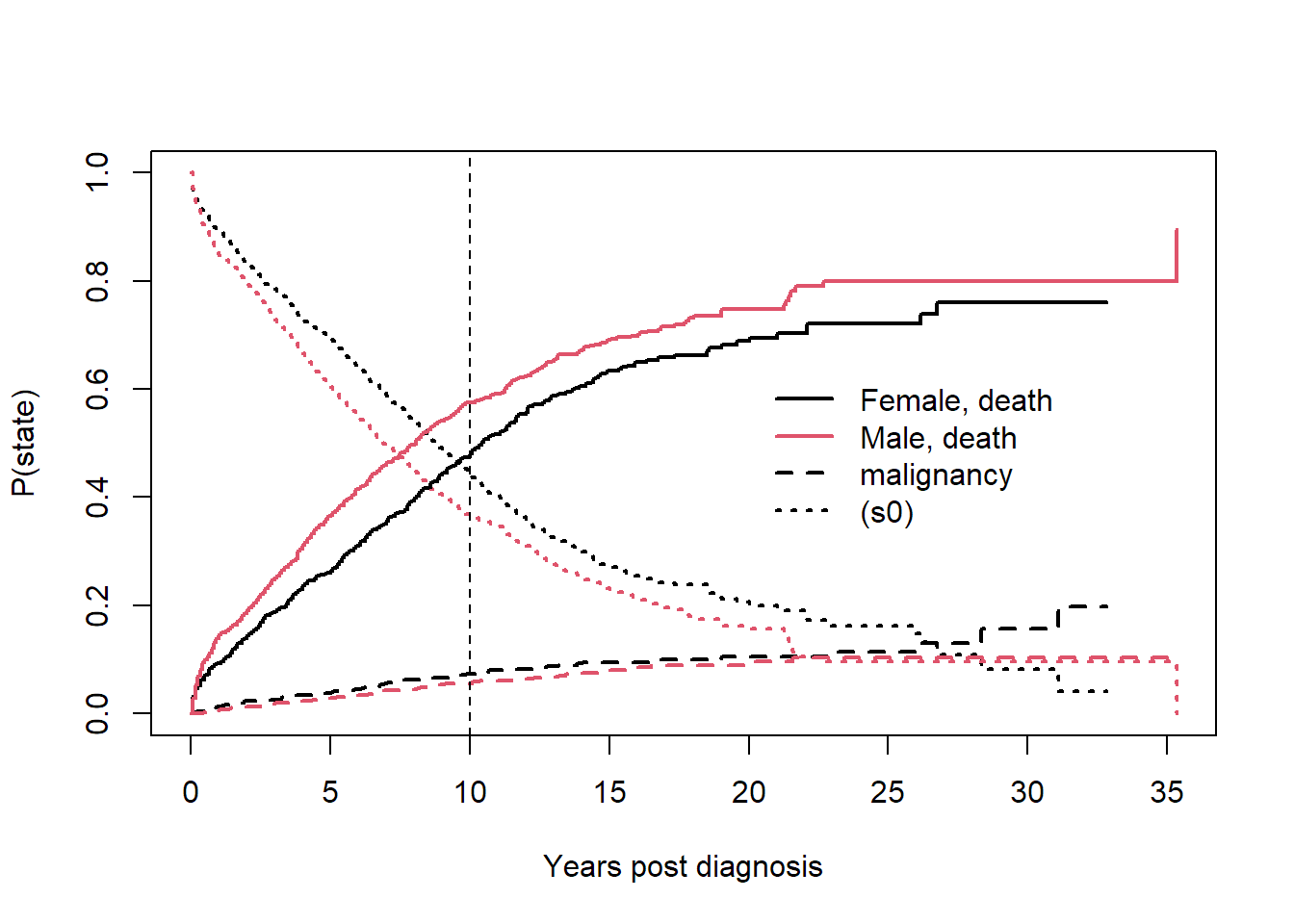
This is the competing risks setting, which can be described with the multi-state model in the figure below.

connect <- matrix(0, nrow = 3, ncol = 3, 
                  dimnames = lapply(1:2, \(i) c("MGUS", "PCM", "Death")))
connect[1, 2:3] <- 1
statefig(c(1, 2), connect)

Suppose we are interested in the effect of the mspike variable on either pcm or death. We fit the following models

mgus2 <- subset(mgus2, !is.na(mspike))

mgcipcm <- cumincglm(Surv(etime, event) ~ mspike, cause = "pcm", time = 120, 
                   data = mgus2)
mgcideath <- cumincglm(Surv(etime, event) ~ mspike, cause = "death", time = 120, 
                   data = mgus2)

which gives us two coefficients for mspike.

Exercise

Write a function to perform simultaneous inference on the two coefficients. That is, find a way to test the null hypothesis that both mspike coefficients (in the pcm model and the death model) are equal to 0.

Solution 1

This solution involves stacking the estimating equations for both models, and the refitting with an indicator for the outcome type.

jointfit <- function(fit1, fit2) {
  
  bform <- update.formula(fit1$formula, .PO ~ .)
  
  dset1 <- get_all_vars(bform[-2], fit1$data)
  dset1$.PO <- fit1$y
  dset1$model <- "fit1"
  dset1$id <- 1:nrow(dset1)
  
  dset2 <- get_all_vars(bform[-2], fit2$data)
  dset2$.PO <- fit2$y
  dset2$model <- "fit2"
  dset2$id <- 1:nrow(dset2)
  
  dset <- rbind(dset1, dset2)
  
  nform <- update.formula(bform, ~ .:model + model - 1)
  
  geefit <- geese(nform, data = dset[order(dset$id),], id = id)
  
  geefit
  
}

jointm <- jointfit(mgcipcm, mgcideath)


mstat <- c(t(jointm$beta[3:4]) %*% solve(jointm$vbeta[3:4, 3:4]) %*% jointm$beta[3:4])
pchisq(mstat, df = 2, lower.tail = FALSE)

## [1] 0.000235711

Solution 2

This solution uses the bootstrap to estimate the covariance matrix of the two coefficients.

B <- 2000
beta.boot <- matrix(NA, nrow = B, ncol = 2)

for(j in 1:B){
 
  mgus2.j <- mgus2[sample(1:nrow(mgus2), nrow(mgus2), replace = TRUE),]
  
  mgcipcm.j <- cumincglm(Surv(etime, event) ~ mspike, cause = "pcm", time = 120, 
                   data = mgus2.j)
  mgcideath.j <- cumincglm(Surv(etime, event) ~ mspike, cause = "death", time = 120, 
                   data = mgus2.j)
  
  beta.boot[j,] <- c(mgcipcm.j$coefficients[2], mgcideath.j$coefficients[2])

}

mstat <- c(mgcipcm$coefficients[2], mgcideath$coefficients[2]) %*% 
  solve(cov(beta.boot)) %*% c(mgcipcm$coefficients[2], mgcideath$coefficients[2])
pchisq(mstat, df = 2, lower.tail = FALSE)

##              [,1]
## [1,] 0.0002151841